" 백준 2839번 설탕 배달 파이썬 풀이 "
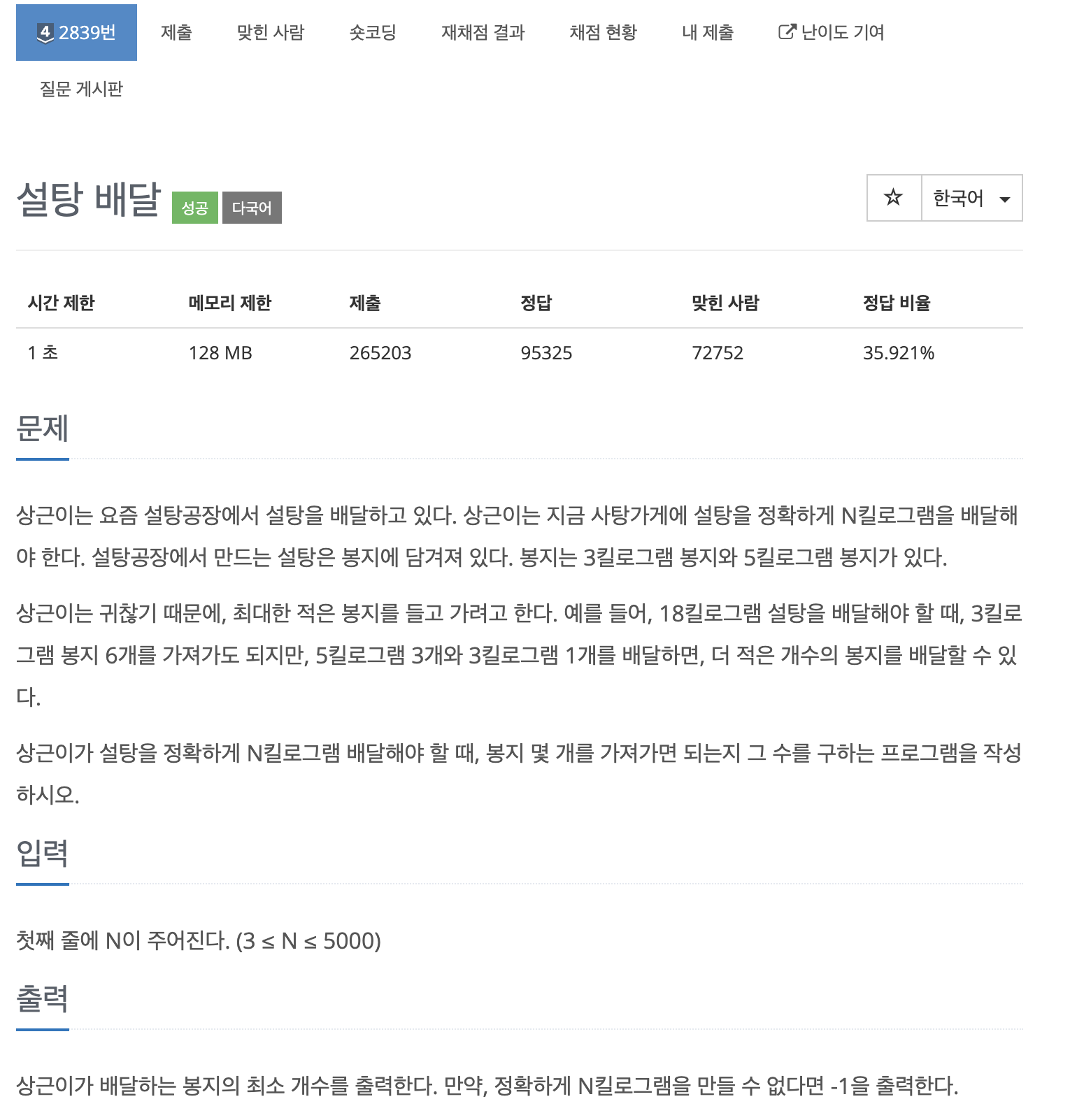
2839번 문제는 다음과 같은 조건을 가진 문제이다
" 문제 조건 "
3, 5kg의 설탕봉지로 정확히 NKg의 설탕을 옮기는 가장 최소한의 봉지 수를 구하기
Nkg을 만들 수 없다면 -1 출력
3 <= n <= 5000
이 문제는 봉지를 옮기는 여러가지 경우의 수들 중 가장 작은 봉지의 수를 구하는 문제이므로 DP(다이나믹 프로그래밍)으로 해결해야하는 문제이다.
그렇다면 어떻게 풀어야할까?
" 💡 문제 해결 아이디어 "
본인은 top-down 방식이 아직 익숙하지 않으므로 bottom-up 방식으로 풀어보았다.
우선 바텀업 방식으로 문제를 해결하기 위해선 dp 테이블을 정의해야한다.
그러기 위해선 dp가 어떤 값을 담을 지 정해야하는데 그 부분은 문제를 통해 어느정도 유추해낼 수 있다.
본인은 dp테이블을 다음과 같이 정의하였다.
dp[i] : ikg을 옮기는 최소 봉지 수
그리고 dp 테이블을 [-1] * (n+1) 로 초기화 해주었다.
만들 수 없는 kg은 -1로 출력해주어야하기 때문에 -1을 기본값으로 초기화한 것이다.
그럼 n은 3이상이라는 조건이 있기 때문에 만들 수 없는 0~2kg 까지는 자동으로 -1처리가 되어버린다.
우리는 이 이후에 알 수 있는 값들을 먼저 초기화해주고 시작하려고 한다.
때문에 3,4,5번을 초기화해주고 시작한다.
3,4,5번 초기화 코드
dp[3] = 1
if n > 3:
dp[4] = -1
if n > 4:
dp[5] = 1
주어진 무게가 3kg, 5kg이므로 3kg,5kg을 만들 수 있는 경우는 결국 1이다. 그리고 4kg을 만들 수 있는 경우는 절대 없기 때문에 -1로 초기화 해준다.
이 과정은 if문을 통해 주어진 n의 값을 봐가면서 수행해야 Index Error가 나지 않는다.
그보다 큰 값들의 경우엔 반복문을 통해 이후의 dp 테이블 값을 구해주면 되는데 조건을 잡아 값을 초기화 해준다.
조건1.
이전 값(현재 값에서 -3한 값과 -5 한 값)이 만들어질 수 없다면?
->
continue
조건2-1.
이전 값(현재 값에서 -3한 값과 -5 한 값)이 만들어 질 수 있다면
->
"현재 값에서 -3한 값을 만드는 데 필요한 최소 봉지 수 +1" 과 "현재 값에서 -5한 값을 만드는 데 필요한 최소 봉지 수 +1" 를 비교하여 더 작은 수를 dp[i] 에 저장
조건2-2.
현재 값에서 -3한 값만 만들어 질 수 있다면
->
"현재 값에서 -3한 값을 만드는 데 필요한 최소 봉지 수 +1" 를 dp[i] 에 저장
조건2-3.
현재 값에서 -5 한 값만 만들어 질 수 있다면
->
"현재 값에서 -5한 값을 만드는 데 필요한 최소 봉지 수 +1" 를 dp[i] 에 저장
if n > 5:
for i in range(6,n+1):
if dp[i-3] == -1 and dp[i-5] == -1:
continue
if dp[i-3] != -1 and dp[i-5] != -1:
dp[i] = min(dp[i-3]+1, dp[i-5]+1)
elif dp[i-3] != -1 and dp[i-5] == -1:
dp[i] = dp[i-3]+1
elif dp[i-3] == -1 and dp[i-5] != -1:
dp[i] = dp[i-5]+1
그리고 최종적으로 dp[n]을 출력해주면 n을 만드는데 필요한 최소한의 봉지 수를 구할 수 있다.
" 코드 "
# 3, 5kg의 설탕봉지로 정확히 NKg의 설탕을 옮기는 가장 최소한의 봉지 수
# Nkg을 만들 수 없다면 -1 출력
# 3 <= n <= 5000
# dp[i] : ikg을 옮기는 최소 봉지 수
n = int(input())
dp = [-1] * (n+1)
dp[3] = 1
if n > 3:
dp[4] = -1
if n > 4:
dp[5] = 1
if n > 5:
for i in range(6,n+1):
if dp[i-3] == -1 and dp[i-5] == -1:
continue
if dp[i-3] != -1 and dp[i-5] != -1:
dp[i] = min(dp[i-3]+1, dp[i-5]+1)
elif dp[i-3] != -1 and dp[i-5] == -1:
dp[i] = dp[i-3]+1
elif dp[i-3] == -1 and dp[i-5] != -1:
dp[i] = dp[i-5]+1
print(dp[n])
'코딩테스트 > 백준' 카테고리의 다른 글
| [백준] 1309번 - 동물원 (파이썬) (1) | 2023.02.06 |
|---|---|
| [백준] 2579번 - 계단 오르기 (파이썬) (1) | 2023.01.31 |
| [백준] 9461번 - 파도반 수열 (파이썬) (1) | 2023.01.29 |
| [백준] 3184번 - 양 (파이썬) (0) | 2023.01.28 |
| [백준] 2606번 - 바이러스 (파이썬) (1) | 2023.01.27 |

